<力の合成のまとめ>
力の合成というと,
①同じ方向に作用する力の合成は足し算
②反対方向に作用する力の合成は引き算
③異なる方向に作用する力の合成は,ベクトルの足し算
として教えます。
私は,これに加えて,
④離れた位置で平行な方向に作用する力の合成
⑤力とモーメントの合成
⑥モーメントとモーメントの合成
の3つを加えて教えた方が力学のスタートにおいて飲み込みやすいと考えています。
その考えで力の合成を説明します。①~③はどの力学の入門書でも書いてあることですし,①②③ともに同じことを言ってますからまとめて説明します。⑤は説明の都合上,「力とモーメント」を,「方向力と回転力」という言葉に置き換えて説明します。

つまり,上記の①~⑥ではなく,
①方向力の合成
②離れた位置で平行な方向に作用する方向力の合成
③方向力と回転力(モーメント)の合成
④回転力(モーメント)と回転力(モーメント)の合成
として説明します。
<①方向力の合成>
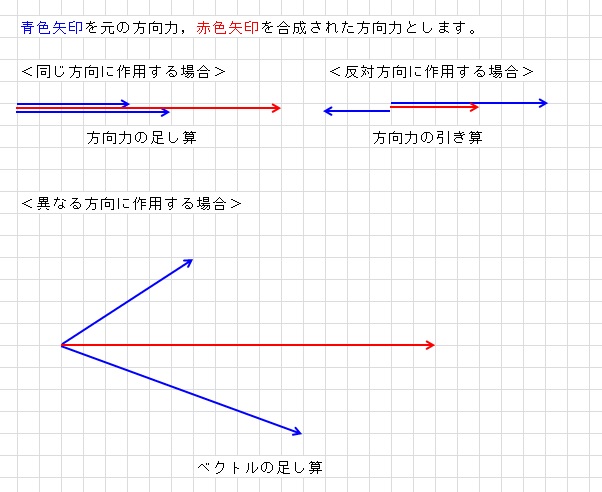
ふたつの方向力が同じ方向に作用したらその合成は,足し算,
ふたつの方向力が反対の方向に作用したら打ち消しあいますからその合成は,引き算,
異なる方向の方向力の合成は,ベクトルの足し算
になります。図解すると次のようになります。
<②離れた位置で平行な方向に作用する方向力の合成>
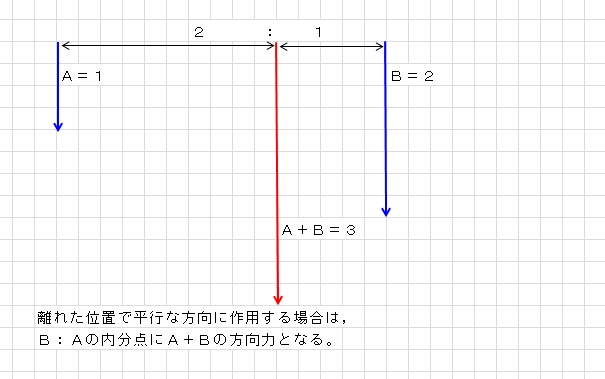
「離れた位置で平行な方向に作用する方向力」とは,例えば天秤の両端に重りをぶら下げた時の両端に作用する方向力のことを言います。上記のように異なる方向に向けられた方向力であれば,作用する交点が必ずありますから交点にベクトルを書いて足し算すれば方向力の合成ができます。でも,平行な方向に作用する場合,交点がありませんから,ベクトルの足し算では合成することができません。平行な方向に作用する場合は,下の図のように合成できます。
<③方向力と回転力(モーメント)の合成>
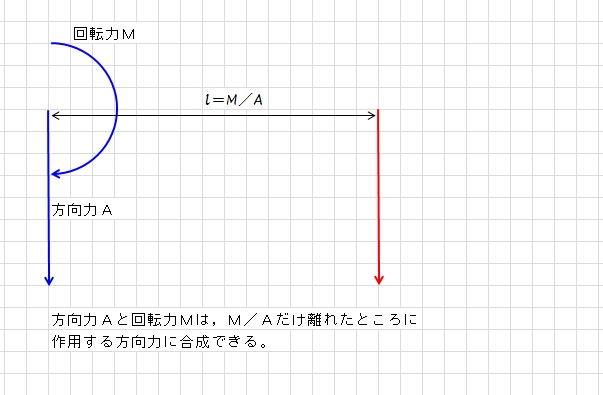
方向力と回転力は合成できます。
方向力Aと回転力Mは,M/Aだけ離れたところに作用する方向力に合成できます。
<④回転力(モーメント)と回転力(モーメント)の合成>
回転力と回転力の合成は,簡単です。同じ方向なら足し算,反対方向なら引き算です。
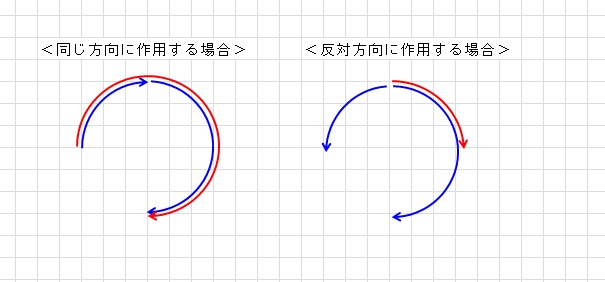
上記は面内に作用する回転力の合成です。
面外に作用する回転力の合成はどうなるでしょうか。面外に作用する回転力とは,例えば,H形鋼の弱軸と強軸に回転力が作用する場合です。通常は弱軸と強軸に分割された回転力に対して断面検定しますから,合成を考える必要はないのですが,あえて合成を考えてみます。答えからいうと,方向力のベクトルの足し算と同じなのですが,回転力の場合は,矢印が円弧を描いていますから,足し算ができません。そこで,回転力の円弧の矢印をその面に垂直な方向に延びる直線の矢印に置きかえます。
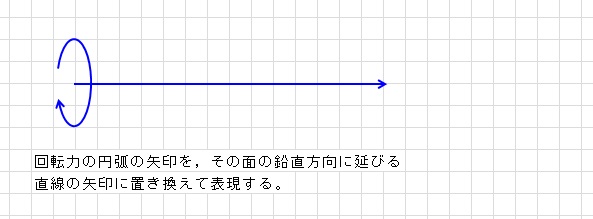
これなら,普通のベクトルの足し算と同じですから回転力の足し算ができます。
ところで「どうしてそのような足し算が成り立つといえるのか」って思いますよね。
それは,2つの回転力をそれぞれ遇力に置き換えて,それは4つの方向力になっていますから,同じ方向の方向力の2つずつを合成してから回転力に置き換えれば,ベクトルの足し算と同じ結果になるからです。図解は省略しますがやってみてください。
[cwpkouzousekkei1]
※ 「モーメント」は,1-④で説明します。1-④「力とモーメント」を見てからもう一度ここへ戻ってください。
私は,離れた位置で平行な方向に作用する場合を,②のように力の合成として教えるべきと考えています。一般的にはそれは,天秤の両端に重りをぶらさげて支点反力を求める問題として提示しますから,取り立てて力の合成とする必要はないのではないかと思われる人もおられるでしょう。でも,そこをもう一歩踏み込んで合成として教えるべきです。力を理解する上で飲み込みやすいと考えます。
③の方向力と回転力の合成は,ほとんど触れられることがありません。〈Ⅰ構造力学(法則・基本的な考え方)〉で紹介する以前には見られなかったと理解しています。方向力と回転力が合成できて,離れた位置に作用する方向力のみで表現できることはとても便利です。例えば,図の梁端には外力として回転力と方向力が作用しています。それを合成するとひとつの方向力になって,その位置は,梁の曲げモーメントが0になる位置です。この図のようなモーメント分布であれば,梁のどこで切ってもそこに作用している方向力と回転力を合成した方向力の位置は同じです。
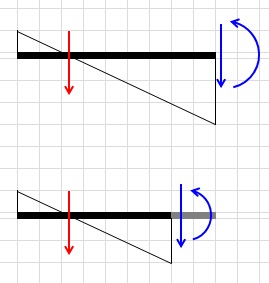
④の回転力と回転力の合成は,単なる紹介です。
[ckouzousekkeilink]
[cwpkouzousekkei2]
このページの公開年月日:2016年3月14日

