Ⅱ 構造躯体として使われる材料の特性(モールの応力円とミーゼスの降伏条件)
モールの応力円
材料力学の中の重要なキーワードとして「モールの応力円」があります。このことなら「材料力学(CAE技術者のための情報サイト)」の「5.2モールの応力円」でわかりやすく解説されていますが,私の感覚で少し補足します。
「モールの応力円って何ですか?」と聞かれた時にどう答えるか。
私は「モールの応力円は,2次元の応力テンソルを図化したもの」なのだと思っています。質量はスカラーです。それは階数0のテンソルです。スカラーは大きさだけを持つものですから棒グラフなどで図化できます。力はベクトルでそれは階数1のテンソルです。ベクトルは矢印で図化できます。方向を矢印の向きで,大きさを矢印の長さで表現します。では,応力テンソルをどうやって図化するか。それがモールの応力円(2次元)です。
モールの応力円は,X軸にσ(引張応力),Y軸にτ(せん断応力)をとって,σ軸上に中心を持つ円を書きます。円がσ軸を切る2点がふたつの主応力の値でありその時はせん断力τは0になります。主応力が生じる面から45度傾けた面ではせん断力τが最大となり,その時のσ(引張応力)はふたつの主応力の平均になっています。
モールの応力円は,その位置と大きさで,その点に生じている応力状態を表現しているのです。ただし,主応力の方向は表現していませんから,σ軸を書くときに最大の主応力の方向にあわせる工夫が必要です。
モールの応力円は,その位置と大きさでその点に作用している応力状態を表現しているものです。
応力が作用していなければ,モールの応力円は原点に半径0の円として表現されます。ここに少しずつ1軸引張の応力,つまりσ2=0でσ1だけを作用させていくと,下のようになります。
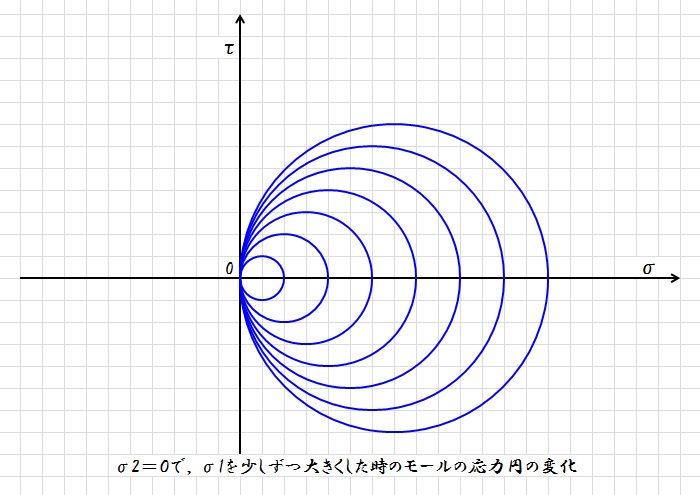
σ2=σ1×0.5となるように少しずつ応力を作用させると下のようになります。
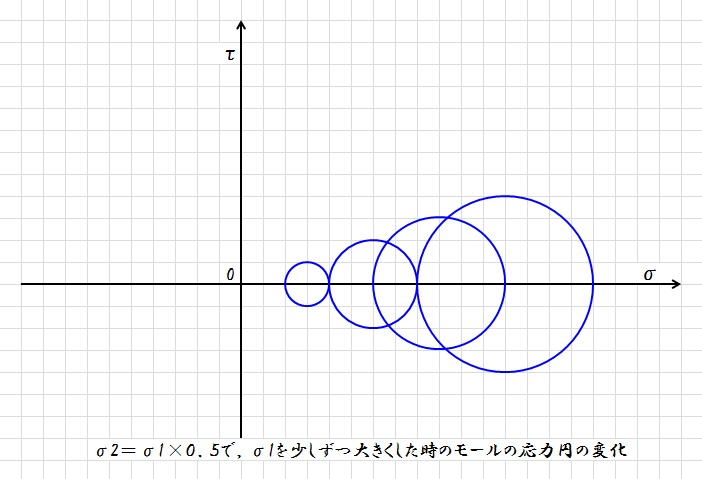
σ2=-σ1,つまり,せん断力のみが生じるように少しずつ応力を作用させると下のようになります。
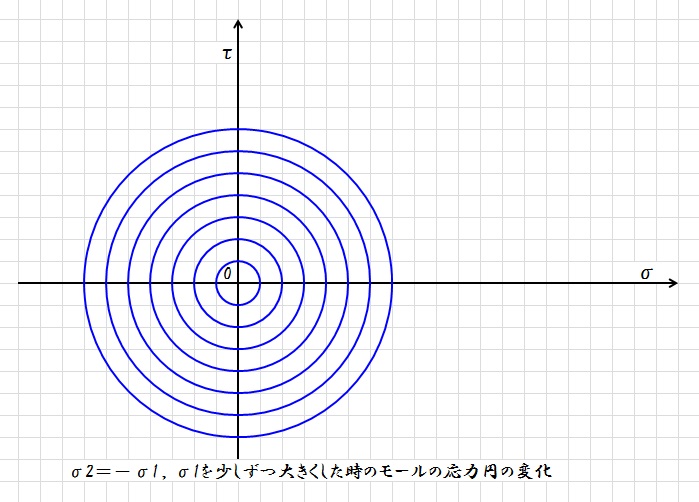
※ モールの応力円を見るときに注意したいのは,円の半径はせん断力を表していますが,円の面積は特に何も表現していないことです。
ミーゼスの降伏条件
次は,材料力学のもうひとつのキーワード「ミーゼスの降伏条件」です。これも「6ミーゼス応力」で解説されています。
ちょっとだけ補足します。
ミーゼスの降伏条件は,2次元,3次元に作用する応力がどのような状態になった時に降伏がはじまるかを示したものです。1次元に作用する応力で降伏する応力がσyであるとわかっている場合に,2次元3次元の応力状態でどのような応力であれば降伏がはじまるかを示すものです。2次元であれば,

となります。
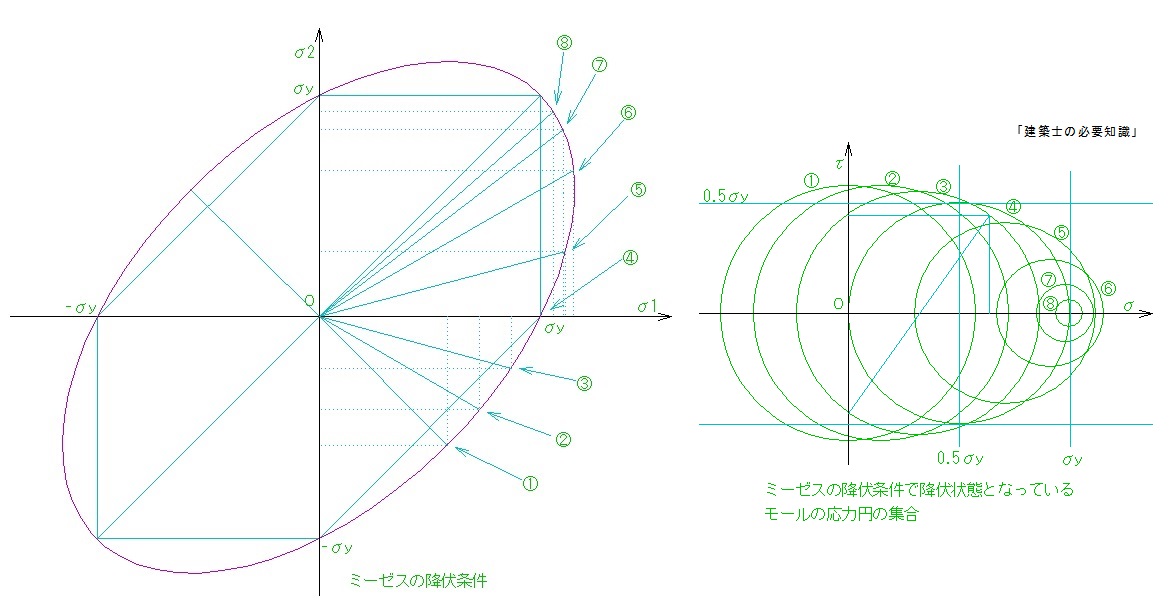
参考までに,モールの応力円とミーゼスの降伏条件を合体させたものを作ってみました。左が2次元のミーゼスの降伏条件で右がミーゼスの降伏条件で降伏状態になっている応力状態のモールの応力円の集合です。
上記のように降伏状態になっているモールの応力円を並べることで何がわかるのか。
このページの公開時点(2015年6月)において,こうしたものを公開しているものは私が探した限りではありません。材料力学の本の中にもなかったように思います。特段に有益ではないから誰も作らなかったのだ,との考えもありますが,「モールの応力円は,2次元の応力テンソルを図化したもの」との前提で降伏状態の応力円を図化して並べたら,何かが見えるのではないかと思いました。で,その結果,何が見えたのか。
純せん断の状態は左の図では①の位置で,図で読み取れるのはσ1とσ2です。その時のせん断力τは読み取れません。右の図ならば,①の円でτが読み取れます。許容せん断力はσy/√3とされていますが,それは,純せん断状態のときのみで,それ以外の状態では小さくなることも読み取れますし,純せん断の①の状態から④までは緩やかな減少でしかないこともわかります。
また,アンカーボルトを引っ張ってさらにせん断力を作用させる場合があります。その状態を③の円の斜め線で表現しました。引っ張り力の直角方向の応力はゼロですからτ軸から伸ばして円の反対側の点をとります。その点が引っ張り力とその時のせん断力です。この状態ならば降伏していて,これよりも小さければ弾性状態です。
こういうことを有益と考えてくれる人がいるかどうかわかりませんが,2次元応力状態の素材特性を考え理解する上でのひとつのトライだと思っています。
[cwpkouzousekkei1]
[ckouzousekkeilink]
[cwpkouzousekkei2]
このページの公開年月日:2015年6月21日