Ⅰ 構造力学(法則・基本的な考え方)
③力の合成と分解の考え方
力の合成は,1点に2つの力を作用した時に,同じ方向に作用させれば足し算したひとつの力が作用したのと同じであり,違う方向に作用すればベクトルに置き換えて足し算した方向の力になる,というやつです。
詳しくは,
「力の合成と分解(輪島実業高校)」がわかりやすいです。
力の合成・分解で注意しなければいけないのは,
- ふたつの力を合成したら,もとのふたつの力はないものとすること
- ひとつの力をふたつの力に分解したら,もとの力はないものとすること
です。
ところで,「力をベクトルに置き換えて足し算,または,分解できるって,どうしてそうなると言えるの?」と思いませんか。「物理の時間に3つのバネ計りを糸でつないでいろんな角度から引っ張って力を計測したらすべてベクトルの足し算に一致した。だから,力はベクトルの足し算に置き換えることができる」となるのですが,それはたまたまそうなっただけで「普遍的にベクトルに置き換えられる」ことを証明したことにはなりません。力の足し算はそういう現象なのであって,証明できないことなんだと思います。
「力の合成と分解」について,もうひとつ大切なことがあります。それは,
「離れた2つの位置に同じ方向に作用する力の合成」です。
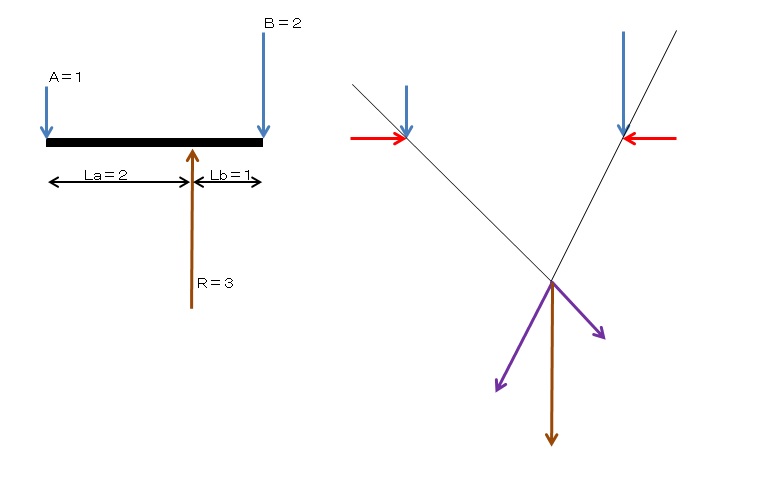
左の図は,シーソーのようなものの両端に下向きの力を作用させてシーソーの支点で反力を生じるというものです。両端の力が1:2であれば,2:1の距離のところに支点を置くとバランスするというものです。なぜそうなるかは,例えば右図のように左右に同じ大きさの反対向きの力(赤)を作用させて,赤と青の合力である紫の力を合力することで,説明できます。
左の図のようなシーソーの両端に力が作用した結果どこに反力が生じるかという問題は,力学的な感覚のわかる人にとっては簡単なことですけど,これを,力の合成として教えておくべきです。力学が苦手な人にとってはこういうところで障壁になっているものと考えられます。「離れた2つの位置に同じ方向に作用する力の合成」やその逆の「分離」は,構造力学の問題を解く中で頻繁に出てきます。
〈力の合成のまとめ〉
[cwpkouzousekkei1]
[ckouzousekkeilink]
[cwpkouzousekkei2]
このページの公開年月日:2015年5月10日

